수식이 깨지면 이 링크에서 보세요.
문제의식
Backpropagation (BP)은 neural network (NN)의 유일한 학습 알고리즘으로 1986년 Geoffrey Hinton의 논문에서 처음 제안되었고 현재까지도 그 명성을 유지하며 널리 사용되고 있습니다. 현재 가장 많이 쓰이는 deep learning (DL) 프레임워크인 Tensorflow (Keras), PyTorch 또한 BP를 기반으로 NN을 학습하고 있으니까요.
하지만 BP에는 문제점이 있습니다.
- 계산량의 부담 - BP는 각 layer의 parameter별 gradient를 모두 계산해야 하므로 계산량이 부담스럽습니다. 현재 NVIDIA의 GPU가 딥러닝의 하드웨어로 쓰는 것은 이때문입니다.
- 비-생물학적인 learning algorithm - 뇌가 BP를 한다는 것은 일견 아직까지는 정설이 아닙니다. 간혹 brain이 BP를 한다는 주장을 하는 연구들이 있지만 이는 소수의견일 뿐입니다.
- Backward를 진행할 때의 대칭 네트워크의 필요 - BP는 계산을 수행함에 있어서 backward mode에서 forward mode와 동일한 네트워크를 필요로 합니다.
등등 많은 문제들이 있습니다. 자세한 문제의식은 이 논문에서 살펴볼 수 있습니다. 따라서 본 글에서는 본인이 고안한 GO-UP (Gradient-based optimization with Ornstein-Uhlenbeck Process)를 살펴봅니다.
(엄밀하지는 않은) 수학적 원리
먼저 gradient descent의 수식을 살펴봅시다:
\[\theta_{t+1} = \theta_{t} - \alpha\frac{\partial L}{\partial\theta_t}\]표준 Gaussian이 아닌 Ornstein-Uhlenbeck process (OUP)는 다음과 같습니다:
\[\frac{\partial\theta}{\partial t}=-k\theta + \eta,\quad\eta\sim\mathcal{N}(\mu,\sigma)\](사실 위 수식은 조금 엄밀성과는 거리가 있습니다.) 이제 위 OUP를 discrete version으로 써 봅시다:
\[\theta_{t+1}=\theta_t-k\theta_t+\eta_t,\quad\eta_t\sim\mathcal{N}(\mu_t,\sigma_t)\]만약 이유는 묻지 말고 위 GD가 OUP를 따른다면 우리는 두 식을 연립할 수 있을 것입니다:
\[\cancel{\theta_t}-\alpha\frac{\partial L}{\partial\theta_t}=\cancel{\theta_t}-k\theta_t+\eta_t,\quad\eta_t\sim\mathcal{N}(\mu_t,\sigma_t)\]결국 우리가 얻는 식은 다음입니다:
\[k\theta_t-\alpha\frac{\partial L}{\partial\theta_t}=\eta_t,\quad\eta_t\sim\mathcal{N}(\mu_t,\sigma_t)\]이제 또 한 번 더 이유는 묻지 말고 $k=\alpha$로 같다고 가정하면
\[\alpha\theta_t-\alpha\frac{\partial L}{\partial\theta_t}=\eta_t,\quad\eta_t\sim\mathcal{N}(\mu_t,\sigma_t)\]가 될 것입니다. 우리가 집중할 것은 위 식입니다. 위 식에서 $\eta_t$를 보기 위해 ResNet에서 아무 iteration, 아무 layer만 꺼내서 $\alpha\theta_t-\alpha\frac{\partial L}{\partial\theta_t}$ 부분을 실제로 살펴보면

빨간색이 $\alpha\theta_t-\alpha\frac{\partial L}{\partial\theta_t}$를 plot 한 것, 파란색이 각 $\alpha\theta_t-\alpha\frac{\partial L}{\partial\theta_t}$의 평균과 분산에 대해서 Gaussian을 fitting한 것으로 이해하시면 됩니다. 놀랍게도 거의 완벽하게 맞는 것을 확인할 수 있습니다. 즉,
$\alpha\theta_t-\alpha\frac{\partial L}{\partial\theta_t}$는 non-standard normal distribution을 따른다
는 것을 확인할 수 있습니다. 이걸 어디다 쓸까요? 바로 뉴럴넷의 학습에 사용할 수 있습니다. 만약 우리가 평균과 분산만 잘 조정하여 $\eta_t$를 추정해낼 수 있다면, $k=\alpha$로 둔다는 가정 하에
\[\theta_{t+1}=(1-\alpha)\theta_t+\eta_t,\quad\eta_t\sim\mathcal{N}(\mu_t,\sigma_t)\]라는 식을 통해 뉴럴넷을 업데이트 할 수 있습니다. 다음 관찰 두 개
\[\mathbb{E}[\eta_t]=\alpha\mathbb{E}\bigg[\theta_t - \frac{\partial L}{\partial\theta_t}\bigg]\]와
\[\text{std}[\eta_t]=\alpha\cdot\text{std}\bigg[\theta_t - \frac{\partial L}{\partial\theta_t}\bigg]\]를 통해 $\eta_t$에 대한 정보가 완벽히 추출 가능하므로 우리는 NN을 학습하는 random한 learning paradigm을 알아낼 수 있는 것입니다.
구현
PyTorch 코드는 다음과 같습니다.
1
2
3
4
5
6
7
8
9
import torch
import torch.nn
outputs = net(inputs)
loss = criterion(outputs, inputs)
loss.backward() # param.grad 계산하기 위해서 필요합니다.
for param in net.parameters():
param.data = (1 - lr) * param + (torch.randn_like(param) \
* torch.std(param - param.grad) + param - param.grad) * lr
이렇게 구현하고 보면 $\theta_{t}\in\mathbb{R}^N$, $\alpha,\sigma_t’\in\mathbb{R}_{\geq0}$, $\mu’_t\in\mathbb{R}^N$인 경우에
\[\theta_{t+1} = (1-\alpha)\cdot\theta_{t} + \alpha\cdot\eta'_t,\quad\eta'_t\sim\mathcal{N}(\mu_t',\sigma_t'I_N)\]로 deterministic term인 $\theta_t$와 stochastic term인 $\eta’_t$의 $(1-\alpha):\alpha$ 비율의 내분점으로 학습을 진행하겠다는 말임을 알 수 있습니다.
실험
실제로 위 코드를 통해 no optimizer, no gradient descent, no backprogagation을 통해 학습하면 다음의 CIFAR10 데이터에 대한 NN의 결과를 얻을 수 있습니다:
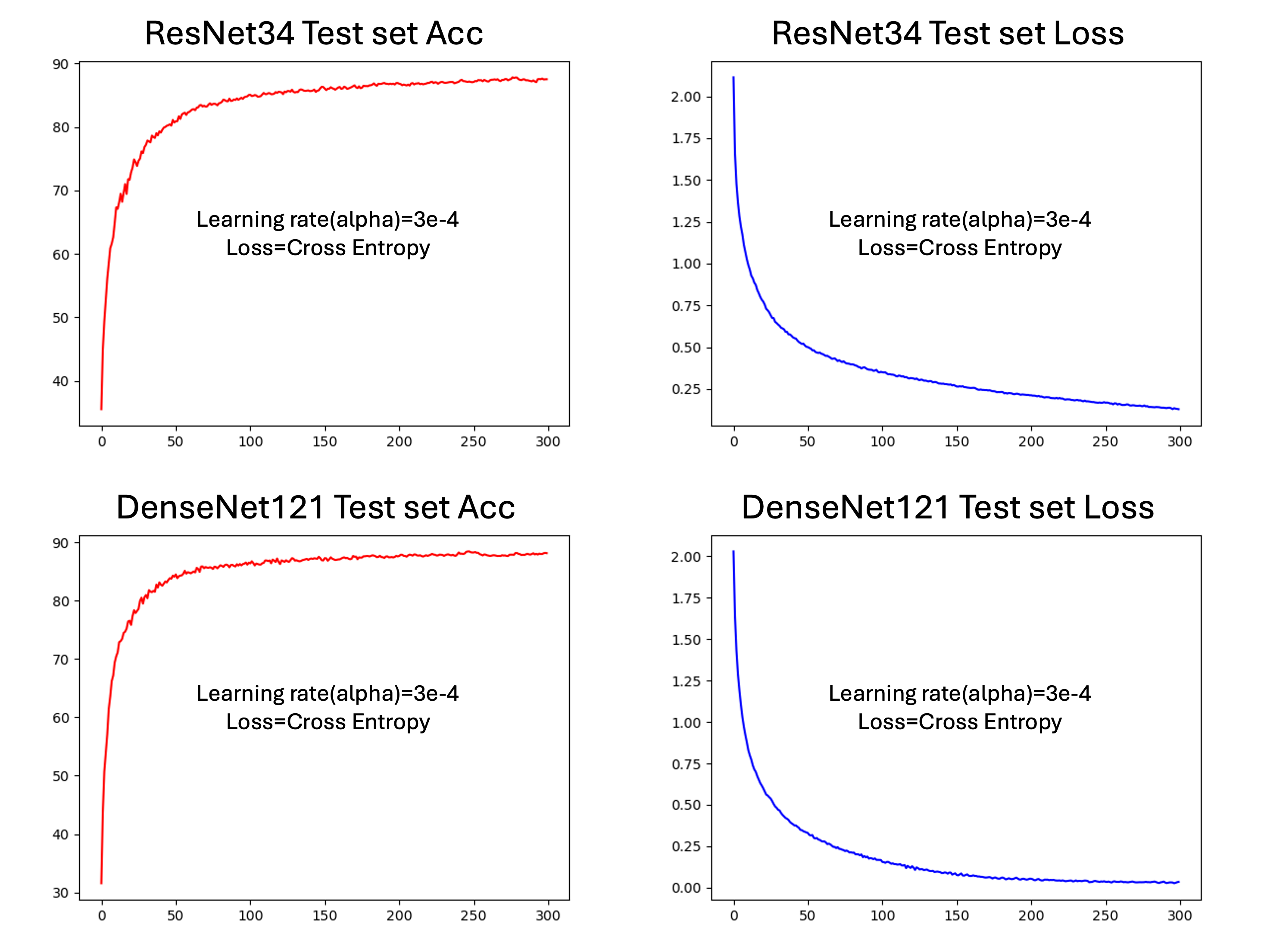
실제로 학습이 됩니다!
논의
GO-UP 알고리즘은 param.grad부분 때문에 어찌 보면 backpropagation을 하는 것처럼 보일 수 있지만 실제로는 gradient-based인 optimization일 뿐이고 backpropagation을 하지는 않습니다.
GO-UP 알고리즘은 BP와 다르게 no optimizer (SGD 기반이긴 합니다만), no gradient descent, no backpropgation의 뉴럴넷 학습 알고리즘입니다.
성능이나 효율성을 차치하더라도 이러한 알고리즘은 BP가 뉴럴넷의 유일한 학습법이 아니라는 것을 증명합니다.
주의사항
논문화를 하고자 할 때는 저자인 장령우(jryoungw2035@gmail.com)에게 연락해주세요. 저자의 동의 없는 연구는 금지합니다.
