그림이나 수식이 깨질 경우 링크에서 확인하세요.
Introduction
수학의 아름다움은 그 추상화에 있습니다. 하지만, 구체적이라고 아름답지 않다거나 중요하지 않다는 것은 아닙니다. 인공지능과 머신러닝 기술이 점점 더 발달함에 따라 고차원 데이터를 분석하는 일은 더욱 중요해지고 우리의 삶에 들어오고 있습니다. 본 글에서는 고차원 유클리드 공간의 반직관적인 행동들에 대해서 살펴봅니다.
High-Dimensional Space
우리가 학교에서 배우는 2,3차원의 저차원 위상공간과는 다르게 고차원 위상공간은 또다른 geometry와 behavior를 가지고 있습니다. 예를 들어, 평균이 0이고 표준편차가 1인 가우시안 데이터를 $d$-차원 고안에서 $n$개 생성하면, 높은 확률로 모든 데이터 포인트들 사이의 거리는 일정합니다. 이러한 이상한 행동들을 살펴보도록 합시다.
The Law of Large Numbers
Random point들을 $d$-차원에서 $n$개 생성하고 이들 사이의 거리를 측정해 봅시다. $y=(y_1,\cdots,y_d)$, $z=(z_1,\cdots,z_d)$로 두고 두 벡터 사이의 거리를 측정하면 다음처럼 나올 것입니다:
\[\|y-z\|^2=\sum_{i=1}^d(y_i-z_i)^2\]이 때 $x_i:=(y_i-z_i)^2$은 iid(independent and identically distributed)가 될 것은 확실합니다. 이러한 경우에 law of large numbers를 적용하면,
\[\text{Prob}\bigg(\bigg|\frac{x_1+\cdots+x_n}{n}-\mathbb{E}[x_1]\bigg|\geq\epsilon\bigg)\leq\frac{\text{Var}(x_1)}{n\epsilon}\]이 됩니다. 이 식은 다음과 같습니다:
\[\begin{align*}\text{Prob}\big(\big|(x_1+\cdots+x_n)-n\mathbb{E}[x_1]\big|&\geq n\epsilon\big)\leq\frac{\text{Var}(x_1)}{n\epsilon}\\\Longleftrightarrow\text{Prob}\bigg(\bigg|\|y-z\|^2-n\mathbb{E}[x_1]\bigg|&\geq n\epsilon\bigg)\leq\frac{\text{Var}(x_1)}{n\epsilon}\end{align*}\]그러면 우변, 혹은 이 확률의 upper bound가 감소할수록, 즉 $n\epsilon$이 증가할수록 좌변의 확률도 감소합니다. 다른 말로 하면, $|y-z|^2$과 $n\mathbb{E}[x_1]$의 차이가 많이 차이날 가능성이 적어진다는 말이지요.
그림을 통해 살펴봅시다. 먼저 100차원에서의 평균 거리입니다. (서로 다른 차원의 벡터간 거리 비교를 위해 차원으로 정규화를 하였습니다.)
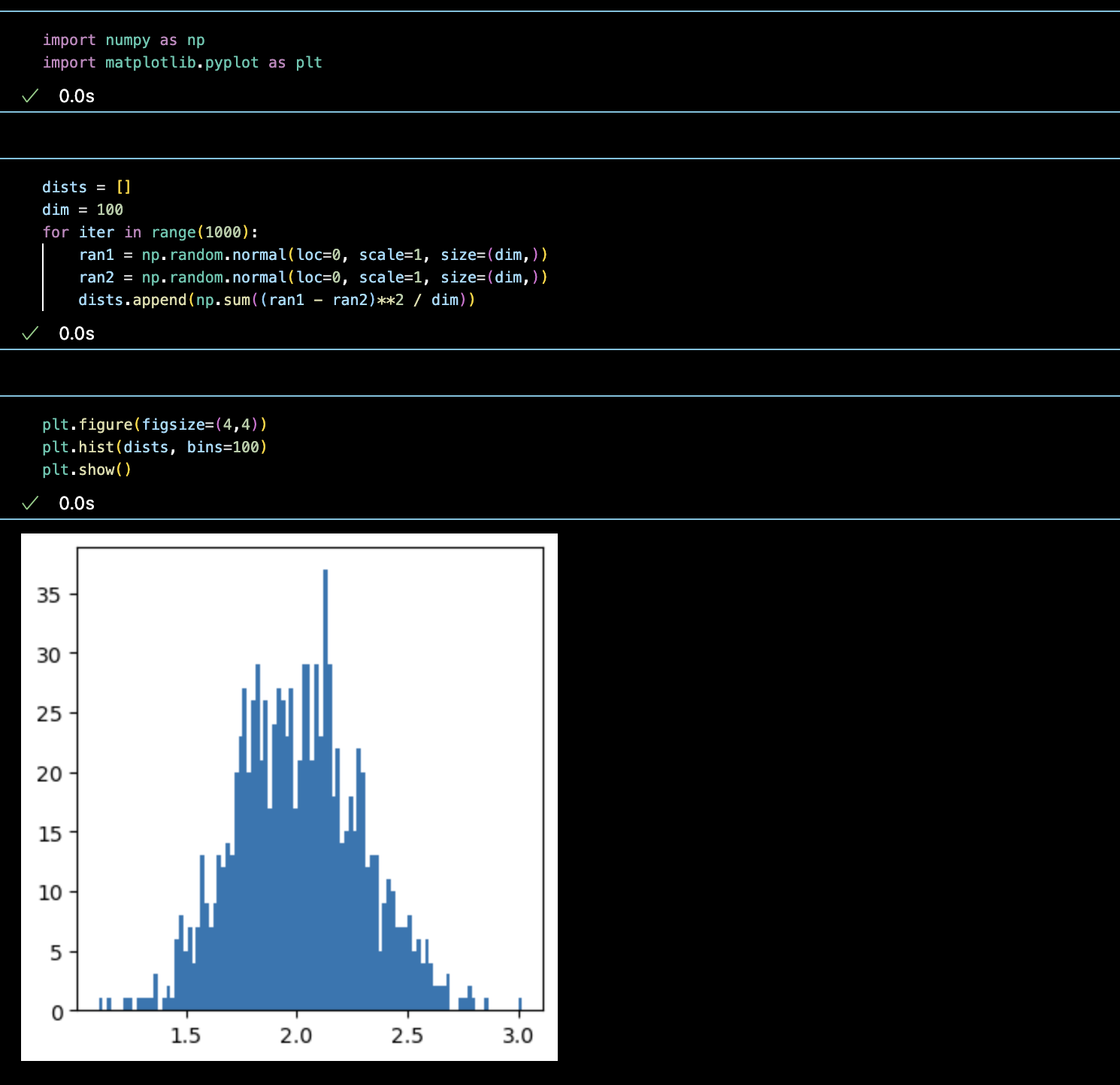
대부분의 데이터가 1.5에서 2.5 사이에 위치하는 것을 살펴볼 수 있습니다. 차원을 10배 해서 1000차원으로 봅시다.
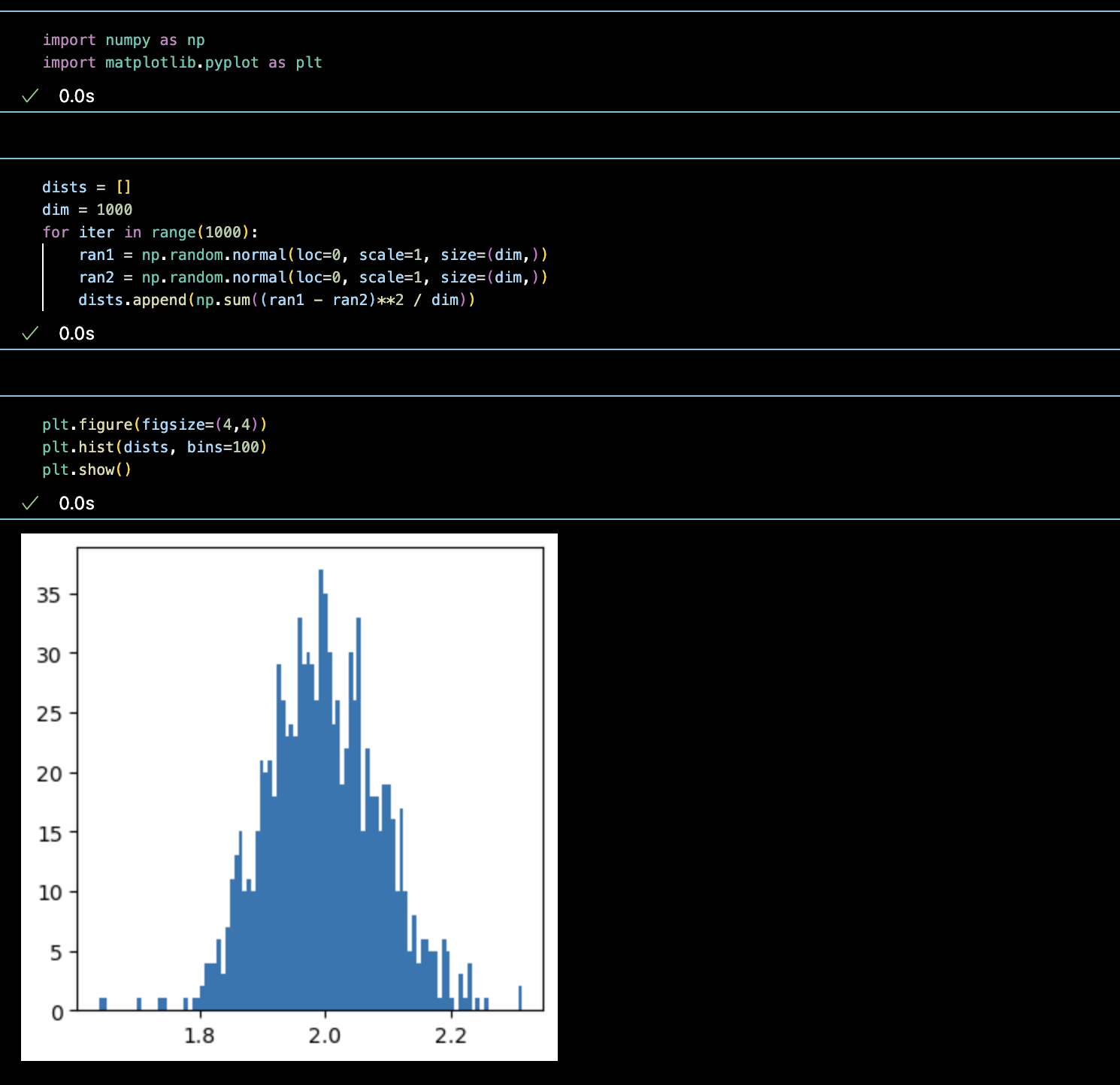
대부분의 데이터가 1.8부터 2.2 사이군요. 실제로 줄어들었습니다. 이제 10배 더 늘려서 10000차원으로 가봅시다.
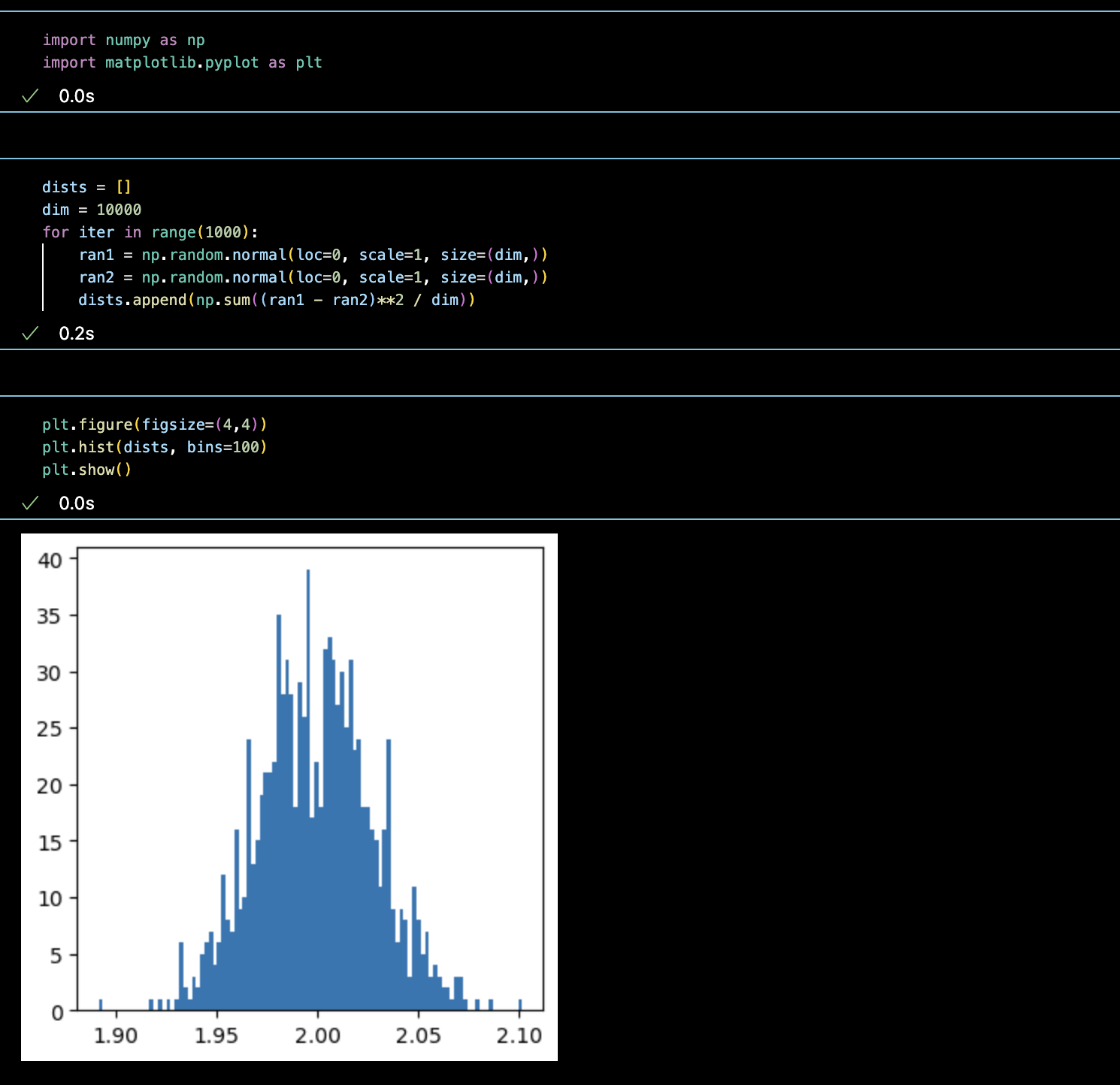
0.05 정도네요. 마지막으로 10만차원입니다.
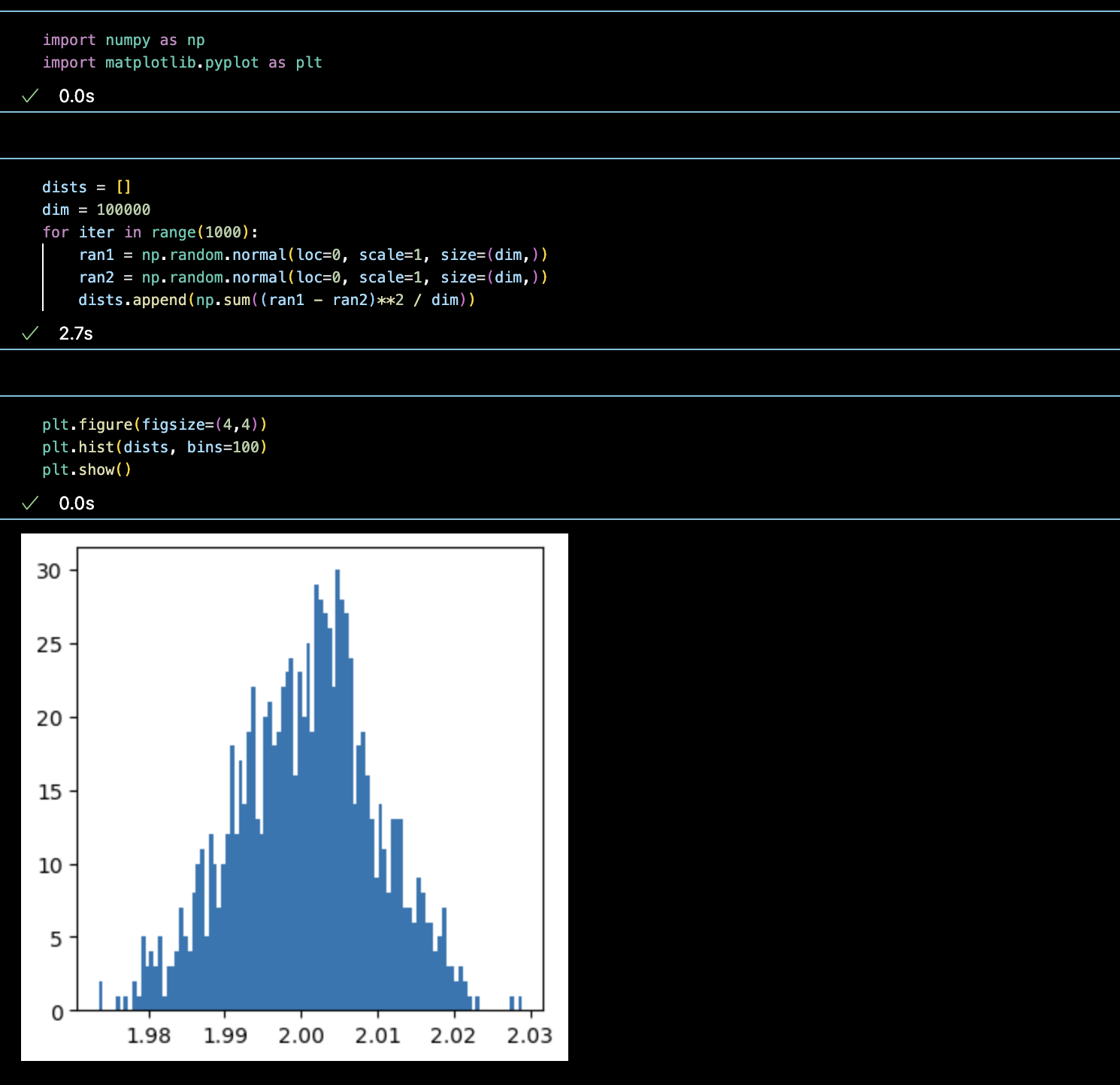
거의 모든 데이터가 모여 있는 것을 확인할 수 있습니다.
The Geometry of High Dimensional Unit Ball
고차원 기하의 특징 중 하나는 대부분의 부피가 바깥 쪽에 몰려있다는 사실입니다. 무슨 말인지 수식을 통해 살펴봅시다.
$A$를 $d$-차원 구라고 하고 $\epsilon$이라는 작은 수 만큼 이 구를 shrink한다고 해 봅시다. 즉, 반지름을 $1$에서 $1-\epsilon$으로 줄이는 것입니다.
그러면 부피는 $\text{Vol}((1-e)A)=(1-\epsilon)^d\text{Vol}(A)$가 되겠지요. 이 때 $\epsilon$이 작다고는 했지만 $d$가 커버리면 $(1-\epsilon)^d$는 거의 0에 가까워지게 됩니다. 즉, 반지름을 조금만 줄이더라도 나머지 부분은 모두 부피가 0이 되어 버리는 것이지요. 결국, 거의 대부분의 부피는 껍질 근처에 있다는 결론을 얻게 됩니다. 다른 접근을 통해 얼마나 빨리 부피가 줄어드는지를 보자면
\[(1-\epsilon)^d\leq e^{-\epsilon d}\]이기 때문에 exponential한 것보다 더 빠르게 감소한다는 사실을 알 수 있습니다.
또한, 단위 구에서는 좀 특이한 일이 일어납니다. 랜덤하게 뽑은 임의의 두 벡터는 거의 항상 수직이라는 것이죠. 먼저 보조정리부터 살펴봅시다. 이제부터 우리는 점을 위첨자로 적을 것이고 성분은 아래첨자로 적을 것입니다.
Lemma
| $c\geq 1$이고 $d\geq3$에 대해서, $d$-dimensional unit ball의 최소한 $1-\frac{2}{c}e^{-c^2/2}$ 비율의 volume이 $ | x_1 | \leq\frac{c}{\sqrt{d-1}}$에 위치해 있습니다. |
proof)
대칭성에 의해서 많아야 $\frac{2}{c}e^{-c^2/2}$의 부피가 공의 절반인 $x_1\geq0$부분에 대해 $x_1\geq\frac{c}{\sqrt{d-1}}$에 위치해 있다는 것을 보이면 됩니다. $A$를 그러한 영역의 부피라고 하고 $H$를 upper hemisphere이라고 합시다. $A$의 부피를 구하기 위해서는 $d-1$차원 구의 부피 $V(d-1)$에 대해
\[\text{Volume}(A)=\int_{\frac{c}{\sqrt{d-1}}}^1(1-x_1^2)^{\frac{d-1}{2}}V(d-1)dx_1\]을 계산하면 됩니다. upper bound를 알기 위해 $x_1\geq\frac{c}{\sqrt{d-1}}$라는 것을 이용합시다. 그러면, $x_1\frac{\sqrt{d-1}}{c}\geq1$이고
\[\begin{align}\text{Volume}(A)&\leq\int_{\frac{c}{\sqrt{d-1}}}^1\frac{x_1\sqrt{d-1}}{c}(1-x_1^2)^{\frac{d-1}{2}}V(d-1)dx_1\nonumber\\ &\leq\int_{\frac{c}{\sqrt{d-1}}}^{\infty}\frac{x_1\sqrt{d-1}}{c}(1-x_1^2)^{\frac{d-1}{2}}V(d-1)dx_1\\ &\leq\int_{\frac{c}{\sqrt{d-1}}}^{\infty}\frac{x_1\sqrt{d-1}}{c}e^{-x_1^2\frac{d-1}{2}}V(d-1)dx_1\\ &=\frac{\sqrt{d-1}}{c}\int_{\frac{c}{\sqrt{d-1}}}^{\infty}x_1e^{-\frac{d-1}{2}x_1^2}V(d-1)dx_1\nonumber\\ &=\frac{\sqrt{d-1}}{c}\bigg[-\frac{1}{d-1}e^{-\frac{d-1}{2}x_1^2}\bigg]^{\infty}_{\frac{\sqrt{c}}{d-1}}V(d-1)\nonumber\\ &=\frac{V(d-1)}{c\sqrt{d-1}}e^{-\frac{c^2}{2}}\nonumber \end{align}\]가 됩니다. 이 때 $(1)$에서 $(2)$로 넘어가는 과정에서는 $(1-t)\leq e^{-t}$가 쓰였습니다.
이제 $x_1=\frac{1}{\sqrt{d-1}}$ 아래쪽의 반구의 부피를 구하면 이 반구는 원기둥에 포함되어 있으므로 원기둥의 부피를 upper bound로 가집니다. $x_1^2+\cdots+x_d^2=1$에서 $\sum_{i=2}^dx_i^2=1-\frac{1}{d-1}$이니 원기둥의 반지름은 $\sqrt{1-\frac{1}{d-1}}$이 됩니다. 더군다나 높이는 $\frac{1}{\sqrt{d-1}}$이기에 구하고자 하는 영역을 $B$라고 하면
\[\begin{align*}V(B)&\leq\bigg(1-\frac{1}{d-1}\bigg)^{\frac{d-1}{2}}\frac{1}{\sqrt{d-1}}V(d-1)\\&\leq\bigg(1-\frac{1}{d-1}\frac{d-1}{2}\bigg)\frac{1}{\sqrt{d-1}}V(d-1)\\&=\frac{V(d-1)}{2\sqrt{d-1}}\end{align*}\]이 됩니다. 따라서,
\[\begin{align*}\text{ratio}&\leq\frac{\text{Upper bound above plane}}{\text{Lower bound of total hemisphere}}\\&=\frac{\frac{V(d-1)}{c\sqrt{d-1}}e^{\frac{-c^2}{2}}}{\frac{V(d-1)}{2\sqrt{d-1}}}=\frac{2}{c}e^{-\frac{c^2}{2}}\end{align*}\]가 되어 원하는 결론을 얻습니다.
Theorem.
| $d$-dimensional unit ball에서 점들을 random하게 $n$개 $x^1,\cdots,x^n$를 뽑는다고 합시다. 그리고 성분을 아래첨자로 적읍시다.그러면 $1-O(1/n)$의 확률로, $ | x_i\cdot x_j | \leq\frac{\sqrt{6\log n}}{d-1}$ for all $i\neq j$ 입니다. |
proof)
위 Lemma에 의하여, $ x_1 \geq\frac{c}{\sqrt{d-1}}$일 확률은 많아야 $\frac{2}{c}e^{-\frac{c^2}{2}}$라는 것을 알 수 있습니다. $d$이하의 자연수 $i$와 $j$에 대해 $x_i$를 북쪽처럼 취급하면 이러한 확률을 만들 수 있는 조합은 $_nC_2$개가 존재하고, 북쪽을 향해서 $j$를 projection했을 때 Lemma에 의해 그 크기가 $\frac{\sqrt{6\log n}}{d-1}$보다 클 확률은 $O(e^{\frac{-6\log n}{2}})=O(n^{-3})$입니다. 따라서 조합까지 고려하게 되면 그러할 확률은 $O(_nC_2n^{-3})=O(n^{-1})$입니다.
Gaussian in High Dimension
1차원 Gaussian은 원점 주변에 mass가 밀집되어 있습니다. 하지만, 고차원이 증가하면 다른 현상이 발생합니다. $d$-dimensional Gaussian with mean $0$, standard deviation $\sigma$는 다음처럼 정의됩니다:
\[p(x)=\frac{1}{(2\pi)^{d/2}\sigma^d}\exp\bigg(-\frac{|x|^2}{2\sigma^2}\bigg)\]이 함수의 값은 원점에서 최대이지만, 우리가 앞에서 살펴본 바와 같이 원점 주변의 volume은 매우 작습니다. $\sigma^2=1$인 경우에, 이 확률을 원점 근처에서 적분하는 것은 거의 무시할 수 있습니다. 따라서 다음과 같은 정리가 등장하는 것이지요:
Theorem (Gaussian Annulus Theorem)
$d$-차원 Gaussian distribution with mean 0, unit variance에 대해서, $x\in\mathbb{R}^n$을 이 분포로부터 뽑았다고 합시다. 그러면 $0\leq\epsilon\leq\sqrt{d}$에 대해서
\[\mathbb{P}\big[\big|\|x\|-\sqrt{d}\big|\geq\epsilon\big]\leq2e^{-\epsilon^2/16}\]입니다.
proof)
$X\sim\mathcal{N}(0,I_d)$을 random vector라고 하고 $X_1,\cdots,X_d$를 그 성분들이라고 합시다. 그러면 $X_i\sim\mathcal{N}(0,1)$인 것을 압니다. 이제 $Y_i:=(X_i^2-1)/2$로 정의합시다. 그러면
\[\begin{align*}\mathbb{P}\big[\big|\|X\|-\sqrt{d}\big|\geq\epsilon\big]&\leq\mathbb{P}\big[\big\|\|X\|-\sqrt{d}\big|\cdot(\|X\|+\sqrt{d})>\epsilon\cdot\sqrt{d}\big]\\&=\mathbb{P}\big[\big|\sum_{i=1}^dX_i^2-\sqrt{d}\big|>\epsilon\sqrt{d}\big]\\&=\mathbb{P}\bigg[\bigg|\sum_{i=1}^d\bigg(\frac{X_i-1}{2}\bigg)\bigg|>\frac{\epsilon\sqrt{d}}{2}\bigg]\\&=\mathbb{P}\big[\sum_{i=1}^dY_i>\frac{\epsilon\sqrt{d}}{2}\big]\end{align*}\]가 됩니다. $\mathbb{E}[X_i]=0$과 $\mathbb{V}[X_i]=1$임을 알고 있으므로
\[\mathbb{E}[Y_i]=\frac{1}{2}\bigg(\mathbb{E}[X_i^2]-1\bigg)=0\]for all $i=1,\cdots,d$ 임을 알고, 2이상의 $k$에 대해 $k$-th moment를 추정해 봅시다. 먼저
\[|X_i^2-1|^k\leq X_i^{2k}+1\]가 성립하기에
\[\begin{align*} |\mathbb{E}[Y_i^k]|&=\bigg|\mathbb{E}\bigg[\bigg(\frac{X_i^2-1}{2}\bigg)^k\bigg]=\frac{1}{2^k}\big|\mathbb{E}\big[(X_i^2-1)^k\big]\big|\\ &\leq\frac{1}{2^k}\int_{\Omega}|X_i^2-1|^k\cdot f(X)dX\\ &\leq\frac{1}{2^k}\int_{\Omega}(X_i^{2k}+1)\cdot f(X)dX\\ &=\frac{1}{2^k}\big(\mathbb{E}[X^{2k}_i]+1\big)\\ &=\frac{1}{2^k}\bigg(\frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}t^{2k}\exp(-t^2/2)dt+1\bigg)\\ &=\frac{1}{2^k}\bigg(\frac{(2k)!}{2^kk!}+1\bigg)\\ &=\frac{(2k)\cdot(2k-1)\cdots2\cdot1}{(2k)^2\cdot(2k-2)^2\cdots2^2\cdot1^2}k!+\frac{1}{2^k}\\ &=1\cdot1\cdots1\cdot\frac{3}{4}\frac{1}{2}k!+\frac{k!}{4\cdot2}\\&=(\frac{3}{4}+\frac{1}{2})\frac{k!}{2}=\frac{k!}{2} \end{align*}\]가 됩니다. 이제 Bernstein’s inequality를 사용하면:
\[\mathbb{P}\bigg[\sum_{i=1}^dY_i>a\bigg]\leq2\exp(-C\min(\frac{a^2}{d},a))\]에다가 $a:=\frac{\epsilon\sqrt{d}}{2}>0$을 대입하고 $\sqrt{d}\geq\epsilon$을 이용하면:
\[\begin{align*}\mathbb{P}\bigg[\sum_{i=1}^dY_i>a\bigg]&\leq\mathbb{P}\bigg[\bigg|\sum_{i=1}^dY_i\geq\frac{\epsilon\sqrt{d}}{2}\bigg]\\&\leq2\exp(-C\min(\frac{\epsilon\sqrt{d}/2)^2}{d},\frac{\epsilon\sqrt{d}}{2}))\\&\leq2\exp(-C\min(\frac{\epsilon^2}{4},\frac{\epsilon^2}{2}))=2\exp(-C\frac{\epsilon^2}{4})\end{align*}\]를 얻습니다.
Conclusion
유클리드 공간은 결국 간단해 보이지만 고차원으로 갈 수록 상식 바깥의 행동을 하는 것을 확인할 수 있었습니다. 따라서 고차원 데이터를 다룰 때는 항상 조심해야 합니다.
Reference
- Alan Blum, John Hopcroft, Ravindran Kannan, Foundations of Data Science
- Sven-Ake Wegner, Lecture notes on high-dimensional data
