Hamiltonian Neural Network
Introduction
Neural Network (NN)은 빠르게 발전해오고 있다. 이러한 NN은 이미지 인식, 강화학습, 로봇과 관련된 분야에서는 특히 그러하다. 이러한 task들의 공통점은 모두 물리적 세계에 기반하고 있다는 것이다. 그렇다면 NN은 물리 법칙을 학습할 수 있는가? 여지껏 알려져온 NN은 물리 법칙을 전제(a priori)로 하지 않아왔다. 오히려, NN의 발전을 살펴보면 그러한 법칙을 주지 않음을 장점으로 삼아오고 있었다고 이해할 수 있다. 하지만 이러한 방법론은 한계점을 가진다. 물리 법칙을 이해하지 못하기 때문에, NN은 노이즈에 취약하다는 단점이 있다.
그렇다면 이러한 부분을 보강하기 위하여 - 그리고 단순 호기심에서라도 - NN이 물리 법칙을 이해할 수는 없는 것일까? Hamiltonian NN (HNN)은 여기서부터 시작한다. 이 논문에서는 물리학자들이 도메인 지식(물리학)을 사용하여 헤밀토니안이라는 물리량을 계산하고 그것으로부터 물리 현상들을 해석하는 방법 대신 NN으로 헤밀토니안을 매개화하고 데이터로부터 직접 헤밀토니안을 학습하는 방식을 취한다. 논문의 표현을 인용하면,
Instead of crafting the Hamiltonian by hand, we propose parameterizing it with a neural network and then learning it directly from data.
를 목적으로 한다고 할 수 있다.
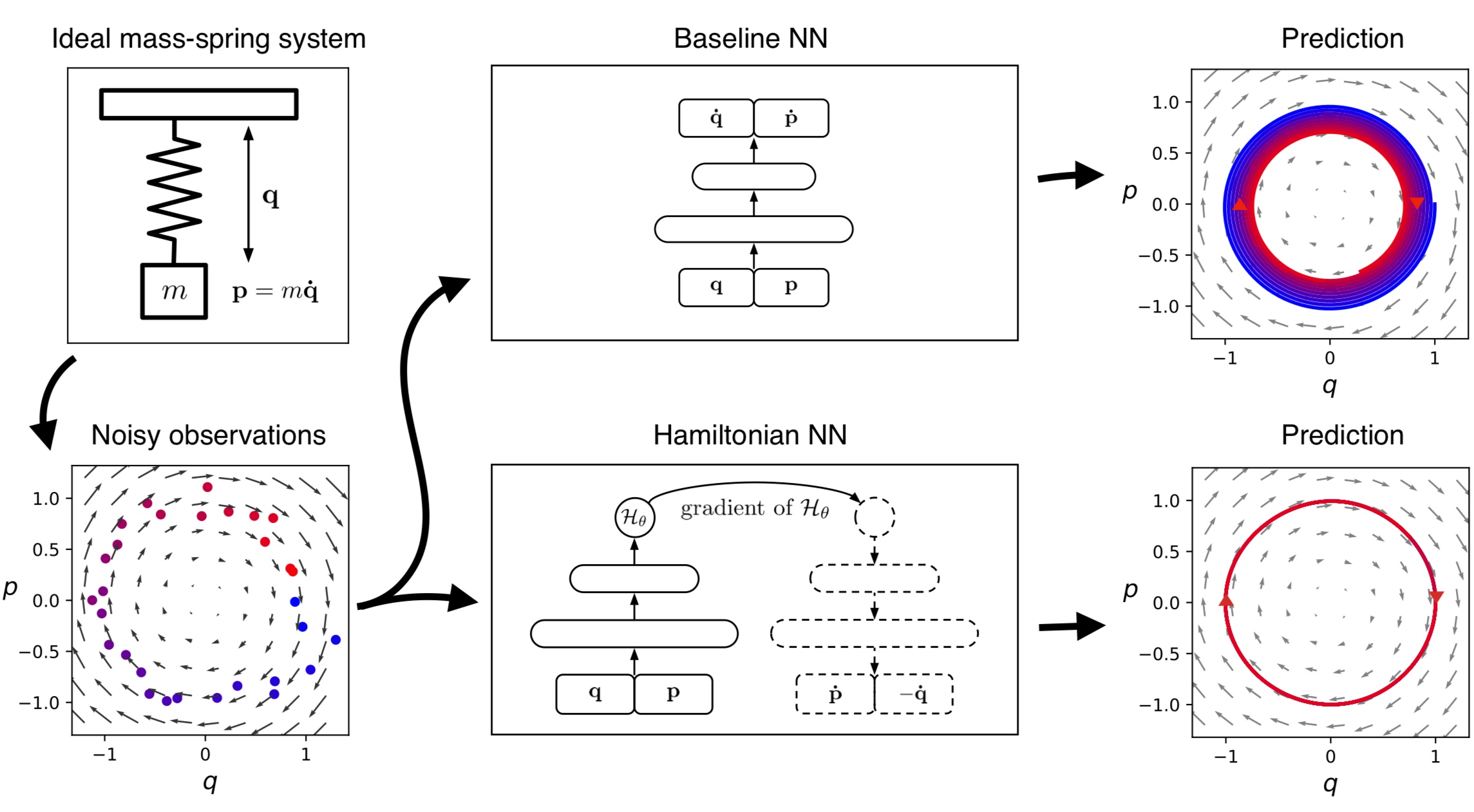
Theory
좋은 물리 모델의 특징을 꼽으라면 변화에 따른 미래를 잘 예측할 수 있느냐가 될 것이다. 즉, HNN에서 하고 싶은 것은 계의 변화를 NN을 통해서 예측하는 것이다. 이의 가장 대표적인 예가 Neural ODE가 될 것이다.
\[(q_1, p_1) = (q_0, p_0) + \int_{t_0}^{t_1}S(q,p)dt\]$\textbf{Hamiltonian Mechanics}$ Willam Hamiltonian은 19세기에 고전역학의 새로운 formulation을 하였다. 이것이 헤밀토니안 역학으로서, 다음과 같은 특징을 갖는다.
- 계는 크게 두 가지의 좌표 $q=(q_1, \cdots, q_N)$과 $p=(p_1, \cdots, p_N)$을 갖는데, $q$는 주로 위치를 의미하고 $p$는 운동량을 의미한다.
- $\mathcal{H}(p,q)$는 다음 미분방정식을 만족한다.
즉, 위 미분방정식은 벡터 $S_{\mathcal{H}} = (\frac{\partial\mathcal{H}}{\partial p}, -\frac{\partial\mathcal{H}}{\partial q})$가 바로 계의 time-evolving quantity를 재준다는 것을 말하고 있다.
$\textbf{Hamiltonian Neural Network}$ HNN 논문에서는, $S_{\mathcal{H}}$대신 $\mathcal{H}$자체를 학습시키는 것을 목표로 한다. 즉, 다음 loss function
\[\mathcal{L}_{HNN} = \bigg|\bigg|\frac{\partial\mathcal{H_{\theta}}}{\partial p} - \frac{\partial q}{\partial t}\bigg|\bigg|_{2} + \bigg|\bigg|\frac{\partial\mathcal{H_{\theta}}}{\partial q}+\frac{\partial p}{\partial t}\bigg|\bigg|_{2}\]를 최소화하는것을 목적으로 한다.
